Pure Mathematics: Geometry Example

The pope asked Giotto di Bondone to display his skills… He drew a perfect circle

Below is Euclid’s definitions, postulates, and common notions from his book, The Elements. These are the things that are assumed to be true and never false in geometry. They may have older wording but take your time and absorb their meaning.

1. A point is that which has no part.
2. A line is breadthless length.
3. The extremities of a line are points.
4. A straight line is a line which lines evenly with the points on itself.
5. A surface is that which has length and breadth only.
6. The extremities of a surface are lines.
7. A plane surface is a surface which lies evenly with the straight lines on itself.
8. A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
9. And when the lines containing the angle are straight, the angle is called rectilineal.
10. When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called perpendicular to that on which it stands.
11. An obtuse angle is an angle greater than a right angle.
12. An acute angle is an angle less than a right angle.
13. A boundary is that which is an extremity of anything.
14. A figure is that which is contained by any boundary or boundaries.
15. A circle is a plane figure contained by one line such that all the straight lines falling upon it from the one point among those lying within the figure are equal to one another.
16. And the point is called the centre of the circle.
17. A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
18. A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
19. Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
20. Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
21. Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
22. Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
23. Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.

Postulates

1. To draw a straight line from any point to any point.
2. To produce a finite straight line continuously in a straight line.
3. To describe a circle with any centre and distance.
4. That all right angles are equal to one another.
5. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

Common Notions

1. Things which are equal to the same things are also equal to one another.
2. If equals be added to equals, the wholes are equal.
3. If equals be subtracted from equals, the remainders are equal.
4. Things which coincide with one another are equal to one another.
5. The whole is greater than the part.

Now, to use what we know, let us look at the statement On a given finite straight line to construct an equilateral triangle. This is Euclid’s first proposition that he proved long ago.

Proposition 1: On a given finite straight line to construct an equilateral triangle

Proof: Let line l₁ be a finite, straight line.

Let points p₁ and p₂ be the extremities of line l₁. Let circle c₁ be centered at p₁ with distance equal to the distance of p₁ to p₂. Let circle c₂ be centered at p₂ with distance equal to the distance of p₁ to p₂.

Let point p₃ be a point where c₁ and c₂ intersect. Let line l₂ be a straight line from p₁ to p₃ and line l₃ be a straight line from p₂ to p₃. Hence, lines l₁, l₂, and l₃ are a trilateral figure T.

So, l₁ is the same length as l₂ since c₁ is a circle and l₁ and l₂ share p₁. Also, l₁ is the same length as l₃ since c₂ is a circle with centre p₂. Since l₂ is the same length as l₁ and l₃ is the same length as l₁, l₂ is the same length as l₃.

Therefore, the trilateral figure T is an equilateral triangle.

This proof may be easier to see if we had some pictures. This is the geometry example after all! Below is the proof above with figures.

Let line l1 be a finite, straight line.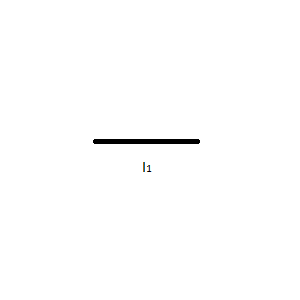
Let points p1 and p2 be the extremities of line l1.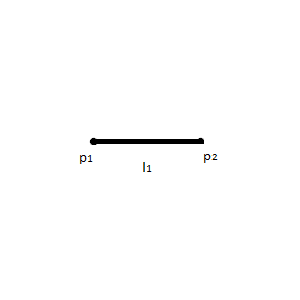
Let circle c1 be centered at p1 with distance equal to the distance of p1 to p2.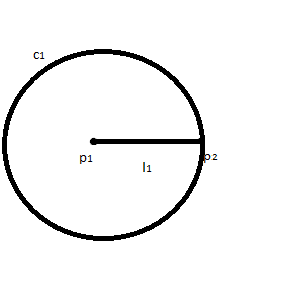
Let circle c2 be centered at p2 with distance equal to the distance of p1 to p2.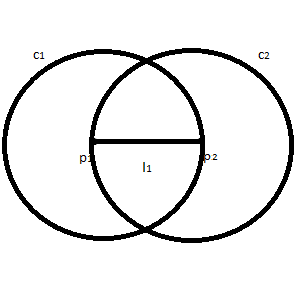
Let point p3 be a point where c1 and c2 intersect.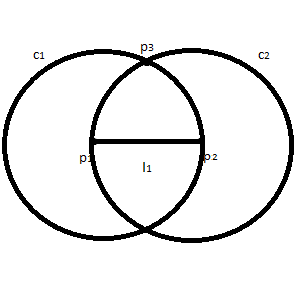
Let line l2 be a straight line from p1 to p3 and line l3 be a straight line from p2 to p3.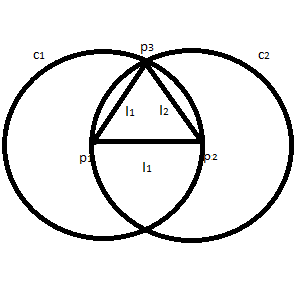
Hence, lines l1, l2, and l3 are a trilateral figure T. So, l1 is the same length as l2 since c1 is a circle and l1 and l2 share p1. Also, l1 is the same length as l3 since c2 is a circle with centre p2. Since l2 is the same length as l1 and l3 is the same length as l1, l2 is the same length as l3. Therefore, the trilateral figure T is an equilateral triangle.

Now that you have an idea of how to prove something mathematically, try proving the next two propositions below. This page has everything that you need to prove them.

To place at a given point a straight line equal to a given straight line.

Given two unequal straight lines, to cut off from the greater a straight line equal to the less.